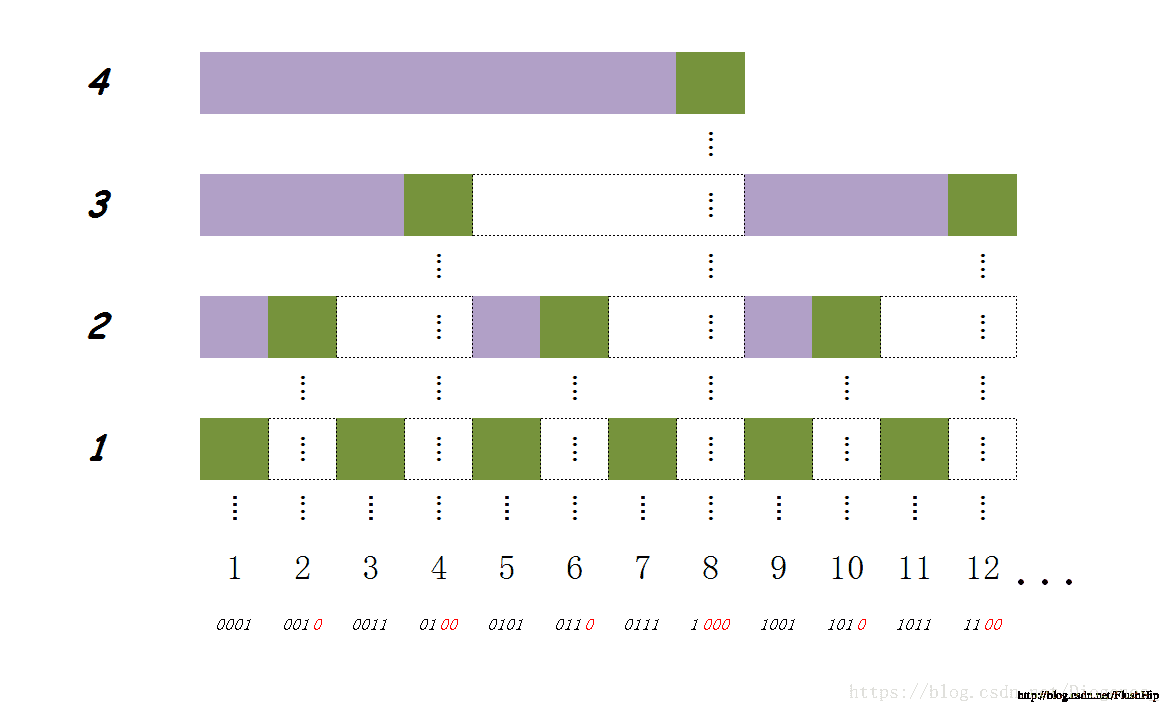树状数组(Binary Indexed Tree),又名二叉索引树,Fenwick树,其处理的问题模型一般可以转化为如下形式:
定义一个数组 $a[1 .. n ]$,并维护一下两个操作:
- 修改,给 $a[i]$ 加上某个增量 $delta$。
- 查询,询问某个前缀 $a[1.. index]$ 的和,即 $ \sum_{i = 1}^{index} a[i]$。
显然,朴素的算法能够在 $O(1)$ 的时间内处理修改操作,但对于查询操作需要 $O(n)$ 的时间复杂度,这在查询次数较多的情况下是接受不了的。而树状数组可以达到在 $O(\log n)$ 的时间内完成修改和查询操作。
我们知道,每个整数可以表示为若干个2的幂次之和。相似的,对于每次求前缀和,我们也希望能够将其分解为一系列恰当的,不相交的”子集”,进而求出它们的和。
举例来讲,$7 = 4 + 2 + 1 = 2^2 + 2^1 + 2^0$ 那么求前缀和 $\sum_{i = 1}^7a[i]$ ,我们也希望能够将它分为 $3$ 个子集的和。一般地,如果前缀下标 $index$ 的二进制中有 $m$ 个 $1$, 我们就希望将其分解为 $m$ 个子集之和。基于这种思想,我们构造如下的表格:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 内容 | 1 | 1..2 | 3 | 1..4 | 5 | 5..6 | 7 | 1..8 | 9 | 9..10 | 11 | 9..12 |
下标代表每个子集的编号,内容表示该”子集”所包含的 $a$ 数组的元素。这样划分的用意何在呢?我们来看一个实际的例子:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a 数组 | 2 | 0 | 1 | 1 | 0 | 2 | 3 | 0 | 1 | 0 | 2 | 1 |
| 前缀和 | 2 | 2 | 3 | 4 | 4 | 6 | 9 | 9 | 10 | 10 | 12 | 13 |
| 子集和 | 2 | 2 | 1 | 4 | 0 | 2 | 3 | 9 | 1 | 1 | 2 | 4 |
这里不妨用 $sum$ 数组表示子集和,接下来,我们检验这种求和方案是否满足一开始提出来的类比思想。
比如,求前缀和 $\sum_{i = 1}^7a[i]$, 我们只需计算 $sum[7]$, $sum[6]$ 和 $sum[4]$,这三项的和,这三个数组中的具体意义可以参考最前面的一张表格,查表发现这三个数覆盖了 $[1, 7]$ 这个区间,而且三个数的和 $3 + 2 + 4 = 9$,说明这种类比方法是成立的!
用BIT经典照片来更直观的理解一下”子集和”的意义:
如上每个长方形代表每个子集对应的部分和,深色代表自己下标对应的值 $a[index]$,浅色部分代表还要维护别的下标对应的值 $a[k .. index - 1]$ 。对于每次查询,如果我们沿着黑色的直线走下去,就可以得到对应的前缀和。
接下来讲实现的过程。
子集的划分方法
现在的问题就是这种子集的划分是如何进行的。列一张表格给出子集和其所包含的元素个数之间的关系。
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 下标的二进制表示 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 |
| 元素个数C | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 |
| C的二进制表示 | 1 | 10 | 1 | 100 | 1 | 10 | 1 | 1000 |
分析上表可以发现原色个数的二进制表示就是下标的二进制表示中的最低位所在的位置对应的书。
现在介绍树状数组实现过程中一个最重要的技术——低位技术($lowbit$)。借助位运算,我们可以得到许多功能强大的 $lowbit()$ 函数。
- $C(index) = index - (index \ and \ (index - 1))$
通过模拟不难发现, $index \ and \ (index - 1)$ 将 $index$ 的最低位1与其之后的0全部变成了0, 这样子再被 $index$ 减去之后,可以得到我们想要的结果,但是事实上我们更常使用的是下面一种求 $lowbit()$ 的方法。 - $C(index) = index \ and \ -index$
这里的 $index$ 要用有符号整形存储。其次,我们知道计算机是用补码存储整数的,正数的补码就是自身的二进制码,其相反数的补码就是用其反码+1而得。我们假设 $index$ 的二进制可以表示为 $\overline{x1y}$ ,其中,$y$ 为若干个0,1就是其最低位的1,那么 $-index$ 则是 $($~$\overline{x})\overline{1y}$,~表示对 $x$ 取非,两者做 $and$ 操作之后就得到了 $\overline{1y}$, 即我们想要的数。
有了上述方法,相信得出模板一定不难。
1 | int c[MAXN]; |
$update()$ 和 $query()$ 分别对应上面两种操作。