【解题报告】Codeforces 786B Legacy

发表于 更新于

传送门

$\text{Solution}$

题目意思很简单，就是你有三种操作：
1 u v w 从u向v连一条权值为w的有向边
2 u L R w 从u向L至R的所有结点连一条权值为w的有向边
3 u L R w 从L至R的所有结点向u连一条权值为w的有向边
首先看到题目，马上就明白不是暴力能够解决的事情（毕竟人家是Div.1的B啊），但是看到L和R，正常人应该都会往线段树这里想一想。没错，标算就是线段树图论建模+最短路。
由于连的是有向边，一棵线段树可能难以满足我们的要求，那就建两棵线段树吧。
举个例子：

样例输入：
4 3 1
3 4 1 3 1
2 1 2 4 2
1 2 3 3
样例输出：
0 2 2 1

样例解释：
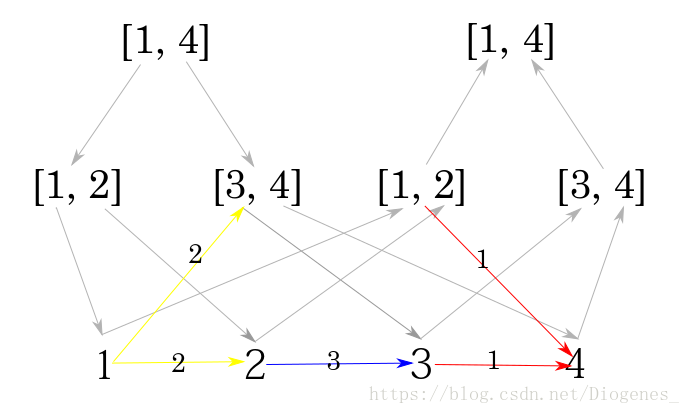
你有三个操作，首先由[1, 3]中所有结点向4号结点连一条权值为1的有向边
其次，从1号结点出发向[2, 4]中左右结点连一条权值为2的有向边，最后，从2到3连一条权值为1的有向边。
写贴一个亲自画的图~
这里写图片描述
看到这张图应该就比较清晰了，给1和2两个操作分别建一棵线段树，加边（具体解释起来有点麻烦，贴代码的时候写写注释解释一下），然后就能很清晰的看到一个图论的模型，然后跑一遍最短路就可以啦~

$\text{Code}$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
#define N 100010
#define M 300110
#define lint long long
#define min(x, y) ((x) < (y) ? (x) : (y))
int n, m, s, cnt, root1, root2;
int head[M], lc[M], rc[M], tot;
struct edge {
	int v, w, nxt; 
}edge[N * 20];
inline void AddEdge(int u, int v, int w) { //在图中添加一条从u连向v的权值为w的单向边
    edge[++tot].v = v, edge[tot].w = w, edge[tot].nxt = head[u]; head[u] = tot; //前向星存边
}
void build1(int &p,int l,int r) { //build关于2操作的线段树
    if (l == r) {
		p = l; //已经是子节点，直接赋值，以便后面加边。
		return;
	}
    p = ++cnt;  //数组模拟链表
    int mid = (l + r) >> 1;
    build1(lc[p], l, mid);
    build1(rc[p], mid + 1, r);
    AddEdge(p, lc[p], 0); //从p向p的左右子树添加一条权值为0的有向边
	AddEdge(p, rc[p], 0); //上图的左边一半的灰色边就是这个build创建的
}
void build2(int &p, int l, int r) { //build关于3操作的线段树
    if (l == r) { 
		p = l; 
		return;
	}
    p = ++cnt;
    int mid = (l + r) >> 1;
    build2(lc[p], l, mid);
    build2(rc[p], mid + 1, r);
    AddEdge(lc[p], p, 0); //从p的左右子树向p添加一条权值为0的有向边
	AddEdge(rc[p], p, 0); //右边一半的灰色边就是这个build创建的
}
int L, R;
void updata(int p, int l, int r, int u, int w, int type) {
    if(L <= l && r <= R) { //完全涵盖直接根据type加边
        type == 2 ? AddEdge(u, p, w) : AddEdge(p, u, w);
        return;
    }
    int mid = (l + r) >> 1;
    if (L <= mid) updata(lc[p], l, mid, u, w, type);
    if (mid < R) updata(rc[p], mid + 1, r, u, w, type);
}
const lint INF = 0x3F3F3F3F3F3F3F3F;
lint dist[M];
std::queue<int> Q;
void SPFA(int s) {  //最短路部分
    memset(dist, 0x3F, sizeof dist);
    dist[s] = 0; Q.push(s);
    while(!Q.empty()) {
        int u = Q.front(); Q.pop();
        for(int i = head[u]; i; i = edge[i].nxt) {
            int v = edge[i].v, w = edge[i].w;
            if (dist[u] + w < dist[v]) 
				dist[v] = dist[u] + w,
				Q.push(v);
        }
    }
}
int main() {
	scanf("%d%d%d", &n, &m, &s);
    cnt = n; //由于建边要求，线段树的结点从n+1开始编号
    build1(root1, 1, n); 
	build2(root2, 1, n);
    while (m--) {
        int opt, u, v, w;
		scanf("%d", &opt);
        if(opt == 1) {
			scanf("%d%d%d", &u, &v, &w);
            AddEdge(u, v, w); //由于上面对叶子结点的处理，这里可以直接加边
        }
        else {
			scanf("%d%d%d%d", &u, &L, &R, &w);
        	updata(opt == 2 ? root1 : root2, 1, n, u, w, opt);
        }
    }
    SPFA(s);
    for(int i = 1; i <= n; i++) 
		std::cout << (dist[i] < INF ? dist[i] : -1) << " ";
    return 0;
}