【学习笔记】可持久化数组

发表于

可持久化数组是由可持久化线段树或可持久化平衡树实现的。这里先给出可持久化线段树的实现方法。

为了方便起见，处理的数组长度为5， 起始的数组元素为1~5，修改是将第一个位置的数组元素改为2。
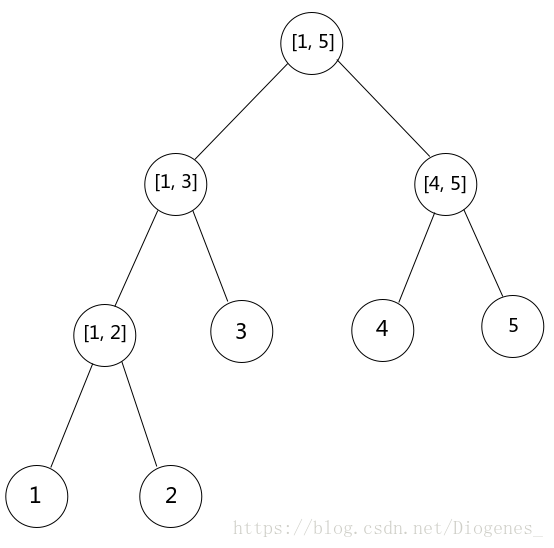
建树规则很简单，只要在叶子节点上写上该点的值就可以了。

先根据原数组建一棵线段树

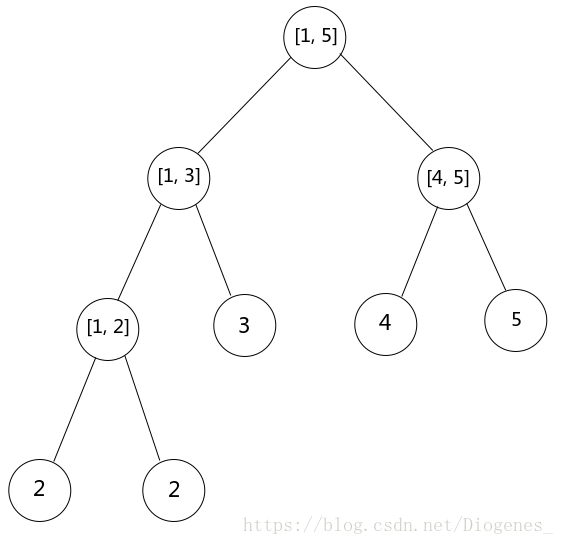
这里写图片描述

第一次修改之后的线段树

这里写图片描述
我们发现，这两棵线段树中只有一个叶子节点的值发生了改变，而操作数非常多，假如每次都memset一下，然后修改一个值，空间上的巨大开销几乎无法想象，那我们可以设想一下，把两个线段树“合并一下”……

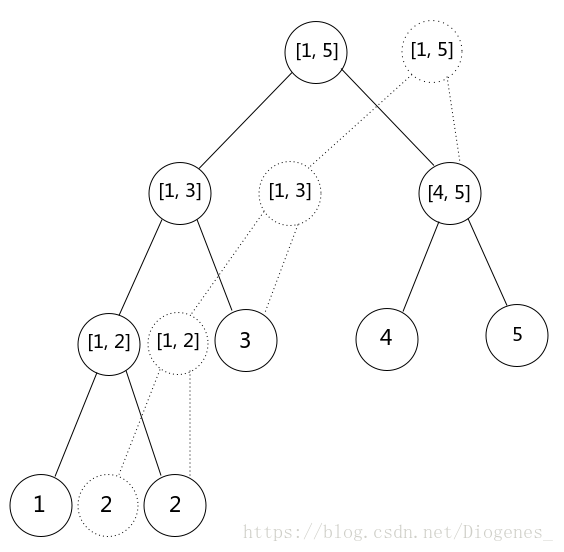
把两次线段树合并的结果

这里写图片描述
这下我们的思路就很清楚了。每次对某个历史版本进行修改时，对于所有包含该位置的区间结点全部新开一个，并与其父节点连边，对于其他结点，由于不需要发生改动，所以直接连接即可。

$Code$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include<cstdio>  
#include<cstring>  
#include<iostream>  
#include<algorithm> 
#include<vector> 
#define maxn 2000005
int n, m, p, x, y, lastans;  
int a[maxn];
inline int getint() {
    int num = 0, sign = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        ch == '-' ? sign = -1 : 1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') 
        num = (num << 3) + (num << 1) + (ch ^ '0'),
        ch = getchar();
    return num * sign;
}
struct Rope { //想不出有什么好名字，，由于c++STL中有支持可持久化的数组rope，就把名字搬过来了。
	static const int MAXSIZE = 2000005;
	int cnt, value[MAXSIZE << 4];
	int root[MAXSIZE << 4], lc[MAXSIZE << 4], rc[MAXSIZE << 4];
	void build(int &k, int l, int r) {  //build
    	k = ++cnt;  //由于结点数目并不固定，采取数组模拟链表而不是类似堆的存储方式存储一棵线段树
    	if (l == r) {
        	value[k] = a[l];
        	return;
    	}  
    	int mid = (l + r) >> 1;  
    	build(lc[k], l, mid);
    	build(rc[k], mid + 1, r);  
	}  
	int query(int k, int l, int r, int pos) {  
    	if (l == r) return value[k];  
    	int mid = (l + r) >> 1;  
    	if (pos <= mid) 
        	return query(lc[k], l, mid, pos);  
    	else return query(rc[k], mid + 1, r, pos);  
	}  
	void insert(int x, int &y, int l, int r, int pos, int val) {  
    	y = ++cnt;  
    	if (l == r) {
        	value[y] = val;
        	return;
    	}  
    	int mid = (l + r) >> 1;  
    	lc[y] = lc[x]; rc[y] = rc[x];  //复制左子树和右子树，那些需要重开的结点会在接下来的递归被修改
    	if (pos <= mid) 
			insert(lc[x], lc[y], l, mid, pos, val);  
    	else insert(rc[x], rc[y], mid + 1, r, pos, val);  
	}  
	void build(int l, int r) { //build函数重载，主程序中调用
		build(root[0], l, r);
	}
	int find(int x, int y, int z) {  //find重载
    	root[z] = root[x];
    	return query(root[x], 1, n, y);   
	}  
	void insert(int x, int y, int pos, int val) { //insert重载
		insert(root[x], root[y], 1, n, pos, val);
	}
};
Rope array;
int main() {  
    n = getint(); m = getint();  
    for (int i = 1; i <= n; i++)
    	a[i] = getint();
    array.build(1, n);  
    for(int i = 1; i <= m; i++) {  
        int x = getint(), opt = getint(), y = getint();  
        if (opt == 1) 
            array.insert(x, i, y, getint());  
        else printf("%d\n", array.find(x, y, i));
    }  
    return 0;  
}

最后，就不带模板的粘一下可持久化数组的模板
由于struct内部有函数重载，有两个版本。

struct版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
struct Rope {
	static const int MAXSIZE = 2000005;
	int cnt, value[MAXSIZE << 4];
	int root[MAXSIZE << 4], lc[MAXSIZE << 4], rc[MAXSIZE << 4];
	void build(int &k, int l, int r) {  
    	k = ++cnt;  
    	if (l == r) {
        	value[k] = a[l];
        	return;
    	}  
    	int mid = (l + r) >> 1;  
    	build(lc[k], l, mid);
    	build(rc[k], mid + 1, r);  
	}  
	int query(int k, int l, int r, int pos) {  
    	if (l == r) return value[k];  
    	int mid = (l + r) >> 1;  
    	if (pos <= mid) 
        	return query(lc[k], l, mid, pos);  
    	else return query(rc[k], mid + 1, r, pos);  
	}  
	void insert(int x, int &y, int l, int r, int pos, int val) {  
    	y = ++cnt;  
    	if (l == r) {
        	value[y] = val;
        	return;
    	}  
    	int mid = (l + r) >> 1;  
    	lc[y] = lc[x]; rc[y] = rc[x];  
    	if (pos <= mid) 
			insert(lc[x], lc[y], l, mid, pos, val);  
    	else insert(rc[x], rc[y], mid + 1, r, pos, val);  
	}  
	void build(int l, int r) {
		build(root[0], l, r);
	}
	int find(int x, int y, int z) {  
    	root[z] = root[x];
    	return query(root[x], 1, n, y);   
	}  
	void insert(int x, int y, int pos, int val) {
		insert(root[x], root[y], 1, n, pos, val);
	}
};

class版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Rope {
	private:
		static const int MAXSIZE = 2000005;
		int cnt, value[MAXSIZE << 4];
		int root[MAXSIZE << 4], lc[MAXSIZE << 4], rc[MAXSIZE << 4];
		void build(int &k, int l, int r) {  
	    	k = ++cnt;  
	    	if (l == r) {
	        	value[k] = a[l];
	        	return;
	    	}  
	    	int mid = (l + r) >> 1;  
	    	build(lc[k], l, mid);
	    	build(rc[k], mid + 1, r);  
		}  
		int query(int k, int l, int r, int pos) {  
	    	if (l == r) return value[k];  
	    	int mid = (l + r) >> 1;  
	    	if (pos <= mid) 
	        	return query(lc[k], l, mid, pos);  
	    	else return query(rc[k], mid + 1, r, pos);  
		}  
		void insert(int x, int &y, int l, int r, int pos, int val) {  
	    	y = ++cnt;  
	    	if (l == r) {
	        	value[y] = val;
	        	return;
	    	}  
	    	int mid = (l + r) >> 1;  
	    	lc[y] = lc[x]; rc[y] = rc[x];  
	    	if (pos <= mid) 
				insert(lc[x], lc[y], l, mid, pos, val);  
	    	else insert(rc[x], rc[y], mid + 1, r, pos, val);  
		}  
	public:
		void build(int l, int r) {
			build(root[0], l, r);
		}
		int find(int x, int y, int z) {  
	    	root[z] = root[x];
	    	return query(root[x], 1, n, y);   
		}  
		void insert(int x, int y, int pos, int val) {
			insert(root[x], root[y], 1, n, pos, val);
		}
};